for Communicators
Checklist for identifying messages with associated uncertainty expressions, and specific guidance for their communication:
If an unqualified conclusion is required, follow the guidance for unqualified conclusions (see Question 5 here). If an unqualified conclusion is not required, state the result of the standardised procedure in the form expressed by the assessors. Also communicate the uncertainty expressions for this message, consulting the respective guidance boxes.
Report the conclusion as expressed by assessors and state that a standardised assessment procedure was followed that takes account of standard uncertainties, and no non-standard uncertainties were identified.
- State that uncertainties exist, using the wording in the scientific output.
Example: “The experts identified limitations in the data on exposure and toxic effects of ZEN and its modified forms” Based on EFSA 2017;15(7):4851
- State that uncertainties exist, using the wording in the scientific output.
- Include in the message a brief description of the sources of uncertainty that have the biggest impact on the respective key messages. (If necessary, consult the assessors to identify these.)
Example: “The experts identified limitations in the data on exposure and toxic effects of ZEN and its modified forms, for example (…)” Based on EFSA 2017;15(7):4851
- Avoid altering the wordings used by assessors to describe the direction and/or degree of uncertainty, or factors contributing to uncertainty (see Question 2 above). Always check the rewording with the assessors if you do.
- State clearly what outcomes and conditions this expression of uncertainty refers to (see Question 1 above).
- Make clear that any uncertainty referred to in the communication has been taken into account in the assessment conclusion.
Example: “The Panel noted that there was very high uncertainty about the exposure estimates and took this into account in its conclusion that there is no health concern” Based on EFSA 2017;15(7):4851
As for entry level, with the following differences: - Before communicating the uncertainty expression, describe a few examples of the evidence/data that were considered and the uncertainties affecting the assessment. – Optionally, mention specific methods that were used in evaluating the uncertainty. – Optionally, mention factors contributing to the overall uncertainty, including the relative importance of individual sources of uncertainty and things like the relevance and reliability of evidence (e.g. in weight of evidence assessments). – Clearly distinguish individual sources of uncertainty from overall uncertainty about the assessment conclusions
Example: “The Panel noted that a high proportion of measurements of ZEN and its modified forms in feed were below the limit of detection, leading to very high uncertainty when estimating exposure” Based on EFSA 2017;15(7):4851
- Communicate clearly that EFSA is unable to give any conclusion on the quantity or question of interest to which this message refers. If the assessment is inconclusive, this implies that nothing further can be said and therefore the communication should avoid using language that might suggest otherwise.
- Indicate very briefly the sources of uncertainty that contribute most to this outcome (e.g. lack of data, poor quality or limited relevance of data).
Example: “EFSA’s experts could not reach a conclusion on the risk for cattle, ducks, goats, horses, rabbits, mink and cats because of a lack of data” Based on EFSA 2017;15(7):4851
- Describe the main sources of uncertainty in more detail, but concisely (following the guidance in Question 2 above).
- Inconclusive assessments are especially likely to include options or requirements for obtaining further data. Communicate these as instructed in UC Section 3.1.6.
Example: “EFSA’s experts could not reach a conclusion on the risk for cattle, ducks, goats, horses, rabbits, mink and cats due to limitations in available data on exposure and toxic effects of ZEN and itsmodified forms, for example (…)” Based on EFSA 2017;15(7):4851
- Report the unqualified conclusion for this message using the same wording as the assessors.
Example: “EFSA’s experts concluded that the exposure to feed containing ZEN ‘in farm situations’ is a low health risk for sheep, dog, pig and fish, and an extremely low health risk for poultry” Based on EFSA 2017;15(7):4851
In this example, the word ‘low’ refers to the conclusion on the level of health risk. There is no expression of uncertainty about this – no indication that the risk might be other than ‘low’, i.e. an unqualified conclusion about the level of risk.
- As for the entry level.
- Optionally, describe briefly how the assessment was made (i.e. what evidence and methods were used to arrive at the conclusions).
- Briefly describe some examples of uncertainties affecting the assessment for this message, as identified in your completed template, consulting Box 4 for guidance on how to communicate this.
- If the assessment contains any verbal or numerical expression of the impact of the uncertainties as identified in your template, follow the respective guidance in Boxes 6–9 below.
- Say that the assessors took the uncertainties into account when reaching their conclusion(s) for this message.
Example: “Following the standard assessment procedure (or ‘Using the evaluation system agreed for contaminants in feed’), experts estimated that high exposure to feed containing ZEN is below the reference value for a health risk for sheep, dog, pig and fish, and well below the reference value for chicken and turkeys. They therefore concluded that the exposure to feed containing ZEN ‘in farm situations’ is a low health risk for sheep,dog,pig and fish,and an extremely low health risk for poultry. In reaching this conclusion, the experts took account of limitations in the data on exposure and toxic effects of ZEN and its modified forms, for example (…)” Based on EFSA 2017;15(7):4851
- State clearly what the probability refers to, including whether it refers to a numerical estimate or a qualitative conclusion. When the probability refers to a numerical estimate, also state the range of the quantity that the probability refers to (see example below).
Example: “The Panel estimates that, under current regulations, the total number of infested tulips in in greenhouses in the EU is 60,000. Based on what is known, the Panel is 50% certain that the number is between 10,000 and 200,000 infested plants.” Based on EFSA 2017;15(8):4879
As for the entry level, with the following differences: - Before giving the probability, describe a few examples of the evidence/data that were considered and the uncertainties affecting the assessment, and state that the experts took these into account when assessing their level of certainty. – Optionally, mention specific methods that were used in quantifying the uncertainty, e.g. modelling, statistical analysis, expert knowledge elicitation (EKE), or a combination of these.
Example: “The Panel performed its assessment using a mathematical model of the entry of nematodes into the EU and their establishment and spread in greenhouse tulips. Uncertainty on the factors represented in the model was quantified by expert judgement, taking into account the limitations of the available data. The Panel estimates…[continue as for entry level]” Based on EFSA 2017;15(8):4879
- State clearly what the probability refers to, including whether it refers to a numerical estimate or a qualitative conclusion. When the probability refers to a numerical estimate, also state the range of the quantity that the probability refers to.
- An approximate probability may comprise a range of probabilities chosen by the assessors from the approximate probability scale, or a different range of probabilities specified by the assessors.
- Always communicate the quantitative range of probabilities because this expresses the assessors’ conclusion without ambiguity. If a verbal expression is also used, present the quantitative probability first (e.g. ‘66–90% certain (likely)’) because it has been shown that this order leads to more consistent understanding than if the verbal expression is presented first (see UC Section 3.1)
- To avoid inconsistency and misunderstanding, do not use the verbal terms in Table 1 to refer to any probabilities or ranges of probabilities other than those shown in this table.
Example: “The experts considered it 66–90% certain (likely) that the increasing proportion of elderly and susceptible people has contributed to the rise in Listeria cases” Based on EFSA 2018;16(1):5134
As for entry level, with the following differences: - Before giving the probability, describe a few examples of the evidence/data that were considered and the uncertainties affecting the assessment, and state that the experts took these into account when assessing their level of certainty. - Optionally, mention specific methods that were used in quantifying the uncertainty, e.g. modelling, statistical analysis, expert knowledge elicitation (EKE), or a combination of these.
Example: “Experts began work on the Scientific Opinion after the 2015 EU summary report on foodborne zoonotic diseases identified an increasing trend of listeriosis over the period 2009–2013. The Panel performed a statistical analysis, which confirmed the increasing trend, and developed a mathematical model of the factors influencing the incidence of infections. Considering the modelling results and the degree of support from indicator data, the experts…’ [continue as for entry level]” Based on EFSA 2018;16(1):5134
- A probability distribution quantifies uncertainty regarding a quantity that has a single true value (not a variable). Graphical representations of distributions are difficult to interpret for non-technical audiences. Therefore, for entry and informed levels, only communicate selected results extracted from the distribution as recommended below.
- State clearly what the distribution refers to (see Section 3.1 General guidance, point 2).
- Provide the central estimate (mean or median), the P5–P95 range (within which it is 90% certain that the true value lies) and/or the P25–P75 range (within which it is 50% certain the true value lies), expressed in such a way that the meaning of the ranges is clear. If it is critical to understanding the message, also give an idea about the form of the distribution behind the range (likelihood associated with particular values/outcomes). If the assessors have provided different quantiles (e.g. P1–P99, see example below), use these instead.
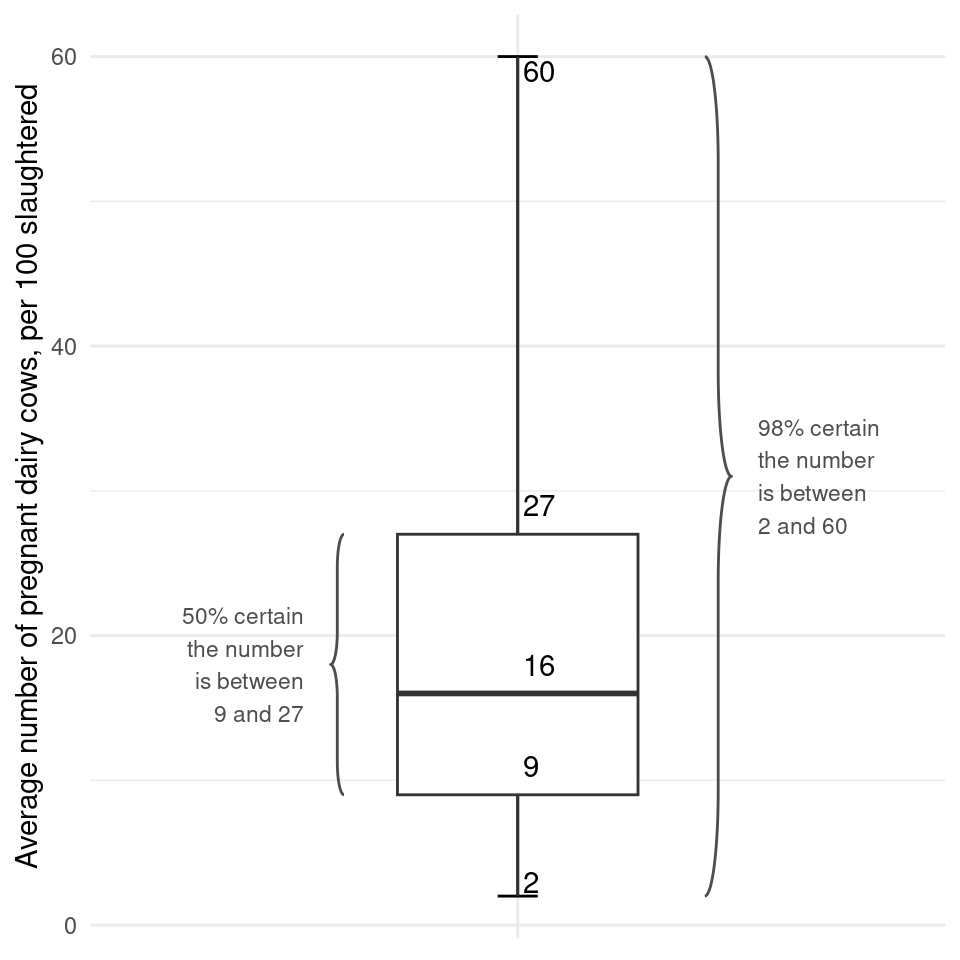
Example: “Experts estimated that, on average in Europe in 2015, 16 out of 100 slaughtered dairy cows were pregnant. Their assessment is based on limited data, but the experts are 50% certain that the European average for 2015 is between 9 and 27, and 98% certain it is between 2 and 60” Based on EFSA 2017;15(5):4782
Note that the example refers to a quantity that is uncertain but not variable: although the average will vary between countries and over time, ‘the European average for 2015’ has a single true value, which is uncertain. For guidance on communicating quantities that are both variable and uncertain, see Question 9 below.
- In addition, or alternatively: if a regulatory (reference) value exists, or a value of particular interest for other reasons (e.g. more than zero occurrence of an adverse outcome), provide the probability of exceeding that value. (See Question 9 for an example of this.)
As for the entry level with the following differences:
- Before giving the results, describe examples of the evidence/data that were considered and the uncertainties affecting the assessment, and state that the experts took these into account in their assessment.
- Optionally, mention specific methods that were used to quantify the uncertainty, e.g. modelling, statistical analysis, expert knowledge elicitation (EKE), or a combination of these.
- Consider providing a visual representation of the uncertainty if this is expected to be useful for understanding, e.g. to aid understanding of the distribution of probability around the central estimate. Use a box plot for this at the informed level. (Do not use graphical representations of full distributions, such as PDF or CDF, in communications for non-technical audiences because these are easily misunderstood.) When using a box plot, explain clearly that it represents the uncertainty, as they are commonly used to represent variability and people may misinterpret them in that way. When including a graphic, provide this in addition to the entry level representation (see above) and not instead of it.
- Label the graphs (including axes, legends, and units) appropriately so that, as far as possible, people will understand them on their own. Accompany every visual with sufficient textual explanation that the informed-level audience will understand it.
Example: “Ten experts from different EU countries each surveyed a sample of slaughterhouses in their country to gather information on the prevalence of animals being pregnant at slaughter in 2015. Six of those experts used the survey results and other available evidence to estimate the average prevalence in Europe for different species in 2015, taking account of the uncertainties involved. The Panel’s conclusions are based on the results. Experts estimated… [continue as in entry-level communication]” Based on EFSA 2017;15(5):4782
When communicating using box or box-and-whisker plots:
- Always accompany box plots with explanations of each element they contain (including central estimate, box and whiskers).
- If there is a value or quantity that is of particular interest to risk managers or the public (e.g. a regulatory/reference value), communicate the probability of the true value being above or below this (depending which is of interest) alongside the box plot, following the specific guidance in Question 6.
Example: “Figure 1 is a box plot summarising the combined judgement of six experts about the average number of pregnant dairy cows per 100 cows slaughtered in the EU in 2015. The horizontal line inside the box is the median estimate: the true average value is considered equally likely to be above or below this estimate. The box and whiskers represent the experts’ collective uncertainty about the EU average in 2015 (not variation between samples of animals). There is 50% certainty that the true average is in the box and 98% certainty it is between the whiskers. There is still a 2% chance that the true average is outside the whiskers” Based on EFSA 2017;15(5):4782
- The term “2D probability distribution” refers here to a distribution that quantifies both variability and uncertainty for the same quantity (e.g. uncertainty about the variability of exposure in a population). Such distributions are difficult to interpret even for technical audiences. Therefore, for entry and informed levels only communicate selected results extracted from the 2D distribution.
- Check with the assessors which results from the 2D assessment are likely to interest the audience, normally one or both of the following:
- The median estimate for a specified quantile of variability, e.g. the 95th percentile, together with a P2.5 and P97.5 (or other quantiles) to represent its uncertainty.
- The median estimate for the frequency of exceeding (or being below) a specified value of the quantity, e.g. the proportion of a population that exceeds a regulatory reference value, together with a P2.5 and P97.5 (or other quantiles) to represent its uncertainty.
- Obtain the selected results from the assessors. The range of values between the two quantiles has a specified probability (95% for P2.5 and P97.5 in the example below), so communicate this following the approach in Question 6.
Example: “The Panel estimated that,if intake of carbendazim from apples and apple products including apple juice was measured for 10,000 UK toddlers on single day schosen at random, including instances where no apples or apple products were consumed, 10 of those intakes would exceed the safe level.The experts are 95% certain that the number of intakes exceeding the safe level would be between 1 and 40 per 10,000” Based on EFSA 2007;5(8):538
The scientific opinion expressed the results in ‘toddlerdays’, which is not readily understandable to non-technical audiences, so it has been reformulated. Other expressions, e.g. number of toddlers per year, might be preferable but are not derivable without additional assumptions. In real communications, the meaning of ‘safe level’ also needs explaining.)
- Before giving the results, describe a few examples of the evidence/data that were considered and the uncertainties affecting the assessment, and state that the experts took these into account in their assessment.
- Optionally, mention specific methods that were used in quantifying the uncertainty, e.g. modelling, statistical analysis, expert knowledge elicitation (EKE), or a combination of these.
- Provide a visual representation of the uncertainty if possible, especially if the uncertainty information is part of the key messages. Use a box plot for this showing median, P5, P25, P75 and P95 for the specific result(s) selected from the 2D distribution. Ask the scientific officer to provide the box plot for the selected result, and communicate it as indicated in Quesion 8.
- Do not use graphical representations of full 2D distributions in entry or informed level communications as many people misunderstand them.
Example: “The Panel developed a mathematical model of the exposure of toddlers to carbendazim in apples and apple products. They used UK data on the occurrence of carbendazim in apples and on consumption of apples and apple products by toddlers. The model computed different eating patterns among toddlers by simulating apple consumption and carbendazim intake for 10,000 ‘toddler-days’ (10,000 random samples from a survey of daily apple consumption by UK toddlers, including records where no apples or apple products were consumed). The simulation also calculated five types of uncertainty affecting the model, e.g. limited measurements of occurrence and consumption, limitations in the precision of the occurrence data. Using this model, the Panel estimated that the number of ‘toddler-days’ in which more than the safe level for carbendazim is ingested from apples and apple products is 10 per 10,000 toddler-days. However, this takes account of only the five sources of uncertainty that were quantified: other uncertainties were taken into account separately by expert judgement” Based on EFSA 2007;5(8):538
Note: after the above text provide information on the experts’ judgement about other uncertainties which the model did not quantify, then go back to to this Questionnaire to identify the type of expression used and locate the corresponding specific guidance for communication.